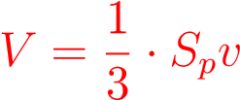A
Interaktívna hračka - robot
Moja Interaktívna hračka je robot postavený zo stavebnice Lego Mindstorm EV3. Môj robot sa dokáže pohybovať po vyznačenej dráhe, uchopiť pohár odniesť ho do koša. Postavil som si ho preto, lebo stále zabúdam po sebe odložiť pohár čo hnevá moju šéfa domácnosti, moju mamku. Tak som rozmýšľal ako si pomôcť. Postavil som si preto robota a naprogramoval som ho tak, aby sa vedel pohybovať po vyznačenej trase po stole, uchopiť plástový pohár a odniesť ho do koša. Stavebnica EV3 ponúka množstvo možností a aplikácii. Pre svojho robota som použil procesor, servo motorčeky, optický senzor a stavebnicové diely.
B
Through the Wall
Construction:
We insert two twisted polarizing foils into the glass tube, which have perpendicular polarization planes so that they overlap by a few mm in the middle of the pipe. The pipe can be closed at both ends with caps or taped after inserting the ball.
Experiment:
We tilt the oven with the ball so that the ball inside slowly rolls down.
Observation:
We will take a close look at the pipeline. A thin partition is visible in the middle, but the ball passes through it without noticing the obstacle.
Theory:
There is no thin partition - that's an optical effect. There are materials through which light can pass in one position/plane and not in another, perpendicular to it. They are called polaroids.
Two polaroid films twisted into tubes create the visibility of the wall.
In the attached photo and video there is a toy in the form of an exhibition experiment.
C
Platónova tělesa
D
Where is the Reflexion
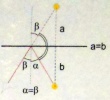
In the middle the chessboard is established glass – with the reflecting coating. Two idencal lamps are on both sides.
Switch one lamp and push it so that its reflection would be combined with the second bulb. The second lamp is necessary only in order to fix the place, where we see the reflection. Look at the second lamp above the glass – that is burns. Compare between themselves distances to the mirror of the burning lamp and its reflection. Now you see, in what the law of reflection consists!
Explanation
Reflexion is located symmetricaly to the plane of the mirror (if to look from aboce).
Distances to the mirror from a subject and its reflection are identifical.
The reflection law says, the angle af incidence is equal to angle or reflection.
How is this connected with the observed equality of distances?
Look the drawing!
E
Guľa farieb
Farby sú v živote človeka dôležité, keďže ovplyvňujú mnohé ľudské činnosti. Napriek tomu o nich vieme málo aj preto, že je málo učebných pomôcok.
Kolormondo je drahá a u nás zatiaľ nedostupná patentovaná učebná pomôcka na učenie farieb.
Zjednodušené Kolormondo spravíme z tvrdšieho bieleho kartónu (napr. z obalov), z ktorého vystrihneme kruhy (dva väčšie a dva menšie) a šesť rovnakých polkruhov. Kartóny postupne na oboch stranách zafarbíme od svetlých po tmavé tóny, pričom prechod vo farebných odtieňoch a sýtostiach môže byť plynulý alebo ohraničený. Do vyschnutých kartónových kruhov vystrihneme symetricky po šesť zárezov smerom do stredu a do polkruhov štyri rovnobežné rovnako veľké zárezy. Dielce navzájom pozasúvame do „gule“.
So zákonitosťami sveta farieb sa takto dá oboznámiť postupne hravo a prirodzenejšie.
F
Precesia
Keď sa spinner roztočí, hrajúci sa drží guľôčku a pokúša sa otočiť spinner z horizontálnej roviny, v ktorej sa točí, do vertikálnej roviny.
Pritom zistí, že zotrvačník si uchováva svoju os otáčania a bráni sa. V spin-stabillized satellites sa práve tento jav využíva na stabilizovanie družíc.
Treba nájsť alebo vyrobiť také zvláštne ložisko.
G
Rovnovážne origami
Skladaním z papiera spôsobom japonských origami vytváram rôzne deťmi obľúbené dinosaury alebo vtáky, ktoré sa v jednom bode udržia napr. na prste.
Dokumentujú tak rovnováhu a ťažisko vytvoreného papierového telesa.
H
Dvojhlavé figúrky
Hracie kocky a figúrky (niekedy označené aj ako kamene) sú základné predmety hier s tisícročnou históriou. Pri hre spoločenských stolových hier (aj edukačného či vedeckého charakteru) sa v súčasnosti bežne používajú jednofarebné plastové figúrky v tvare oblej postavičky s hlavou a telom.
Navrhujem vyrobiť dvojfarebné figúrky, ktoré po otočení o 180o budú mať hore inú farbu ako pôvodne/pred otočením a tým budú môcť mať aj novú úlohu či hodnotu. Dvojhlavá figúrka vznikne spojením dvoch rôznofarebných vrchnákov z PET-fliaš, napr. ich zoskrutkovaním, zlepením, pretiahnutím závlačky...
V súčasnosti, keď výrazne klesá manuálna zručnosť detí a mládeže, bude prínosom, že dvojhlavé figúrky si hráči pred hrou sami vyrobia z odpadového materiálu.
Použitie dvojhlavých figúrok môže zásadne a kreatívne rozšíriť počet stolových spoločenských hier a prispieť k ich vtipnosti/pútavosti. Ak sa pri hre počítajú políčka či iné hodnoty, s výhodou možno používať na hádzanie čísel guľôčku s vnútornou záťažou, ktorá má na povrchu sústredené bodky (jednu až šesť) oproti sebe ako na bežnej šesťbokej kocke miesto nej.
Návod na využitie dvojhlavých figúrok (kameňov) v originálnej hre „2 v 1“.
Počet hráčov: 2 Vek: asi 5+
Hracia doska: 5x7 políčok rozmerov 4x4 cm na výkrese formátu A4
Kamene: každý hráč má 10 dvojfarebných kameňov a 1 „blokovací" svojej farby
1. variant
Každý hráč si postaví svojich 10 kameňov do dvoch radov pred sebou podľa vlastného uváženia zeleným/bielym alebo červeným vrchnákom nahor. Kameňmi sa pohybuje podľa vrchnej farby po voľnej línii (aj dozadu): zeleným/bielym len pravouhlo a červeným len diagonálne. Ak počas hry pre zamýšľaný krok nevyhovuje vrchná farba kameňa, je možné ako samostatný krok kameň obrátiť a tiež neskôr podľa potreby ho ako samostatný krok obrátiť späť. Kamene sa nepreskakujú ani nevyhadzujú a hráči sa v jednotlivých krokoch striedajú.
Cieľ: dostať ako prvý všetky svoje kamene do dvoch radov na protiľahlú stranu v ľubovoľnom poradí a umiestení.
2. variant
Každý hráč si postaví svojich 10 kameňov do dvoch radov pred sebou svojou farbou nahor. Kameňmi sa pohybuje vždy len o jedno voľné políčko ľubovoľným smerom alebo preskočením vedľajšieho kameňa. Preskočením súperovho kameňa je tento vyhodený, ale preskočením svojho nie. Hráči sa v jednotlivých krokoch striedajú.
Cieľ: vyhodiť čo najviac alebo všetky súperove kamene.
Doplnok
Každý hráč má aj jeden vrchnák svojej farby, tzv. „blokovací", ktorý môže použiť kedykoľvek počas hry, ale vždy len ako samostatný krok:
- položiť ho na vhodné voľné políčko a tým ho zablokovať (okrem dvoch radov svojich alebo súperových štartovacích políčok pri 1. variante), vtedy to políčko nie je možné ani preskočiť, ani tam položiť kameň;
- preložiť ho na iné políčko;
- položiť ho dočasne na svoj kameň pri 2. variante - vtedy je kameň nevyhoditeľný, ale ani sa nemôže hýbať, ani ho nemožno preskočiť;
- dočasne ho dať mimo hry;
- vymyslieť a dohodnúť si iné pravidlo.
I
Žabuľa Kvakuľa
Potrebný materiál:
Stará tenisová loptička, nožnice a chuť vyrobiť si žabuľu-kvakuľu.
Popis výroby a použitia:
Tenisová loptička, môže byť aj roztrhaná, sa rozreže na polovicu. Potom sa po obvode uberie cca 5 mm. Žabuľa sa vyskúša - či skočí. Ak neskočí, uberieme ďalší 1mm zhora a opäť žabuľu vyskúšame. Takto pokračujeme, až kým žabuľa začne skákať. Ideálny stav: žabuľa vyskočí „po chvíli" na to, ako ju stlačenú položíme na rovný povrch. Hranie s vlastnoručne vyrobenou žabuľou-kvakuľou je na pripojenom videu.
Teória:
Stlačením/pretlačením kvakule sa žabuľa dostáva do prechodného stavu, v ktorom sa potenciálna energia stlačenej gumy pôsobením pamäťového efektu gumy snaží vrátiť žabuľu do statického stavu. Prebieha postupná premena potenciálnej energie na kinetickú - žabuľa sa pripravuje na svoj skok. V určitom momente dôjde k skokovej premene zvyšku energie - a žabuľa vyskočí. Ak sa žabuľa dlhší čas nachádza v prechodnom stave, materiál si „zvykne" a žabuľa „zlenivie". Dôležitým faktorom je aj teplo. Ak na žabuľu svieti slniečko, žabuľa „nazbiera dosť síl" a vyskočí! (tepelná rozťažnosť gumy).
Prínos:
Ušetrí 2 Eurá (proti produktu Flying Tigger) a zároveň zníži odpad, keďže je vyrobené z roztrhanej loptičky.
J
Hydraulická ruka
Vedecká hračka, ktorá bola navrhnutá a vytvorená pomocou 3D tlače prezentuje spôsob činnosti hydraulickej ruky, ktorá využíva princíp pohonu založený na tlakovej energii a fyzikálnej nestlačiteľnosti kvapaliny. Zábavnou a hravou formou je možné simulovať jej činnosť. Hračka využíva princíp činnosti dvojčinných priamočiarych hydraulických motorov. Hračka je navrhnutá v 2 častiach: Jednou z nich je ovládač, na ktorom sú 4 striekačky, ktoré stlačením prenášajú kvapalinu cez hadičky do jednotlivých častí ramien hydraulickej ruky, ktoré sú spojené otočným spojom. Ruka vďaka jednotlivým pákam ovládača sa dokáže otáčať, dvíhať ramena a otvárať/zatvárať čeľuste pre uchopenie nákladu.
K
Transformer vedeckých hračiek
Pre viac informácií prejdite na webovu stránku: Kúzelná fyzika - Transformer vedeckých hračiek
Experimenty:
- Vĺčik – Gyroskopický efekt, trajektória, precesný pohyb (precesia) (1:00)
- Blikajú nám svietidlá? – Stroboskopický efekt (3:03)
- Vnímanie farieb – miešanie farieb (5:49)
- Ako fungujú hlasivky – Bernoulliho princip, zvuk (9:15)
- Reaktívny motor – Tretí Newtonow zákon (11:35)
- Vznášadlo – trenie (13:06)
- Frndžala – torzné kyvadlo (14:29)
- Jojo – upravené Maxwellovo kyvadlo (16:56)
- Eulerov disk – dynamika valiveho disku na rovnom povrchu (18:27)
L
Kocka z troch ihlanov
Navrhla a vyrobila som učebnú pomôcku, ktorá má podobu drevenej hračky. Žiaci/deti ňou môžu manipulovať, poskladať kocku. Pri manipuláciu sa dá vysvetliť prečo je vo vzorci pre výpočet objemu ihlana jedna tretina.
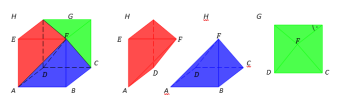
Jedna tretina súvisí s tým, že hranol (drevená kocka) sa dá rozložiť na tri neprekrývajúce sa ihlany. Dôležité je aby každý z ihlanov mal rovnaký objem. Keďže objem hranola je V = Sp.v, objem jedného ihlana je tretinou objemu hranola. Žiaci si nevedia predstaviť, ako „dať“ do hranola tri rovnaké ihlany. Ukázať sa to dá na tejto kocke. Vytvorila som z nej tri rovnaké štvorboké ihlany. Hlavným vrcholom všetkých ihlanov je jeden vrchol kocky (F). Jeden z ihlanov má za podstavu dolnú stenu kocky, druhý zase ľavú bočnú stenu kocky a pre posledný je podstavou zadná stena kocky.Pozri na obrázok:
Dostala som tri štvorboké ihlany ABCDF, ADHEF a CDHGF, ktoré majú rovnaké podstavy. To preto, lebo sú to štvorce ABCD, ADHE a CDHG. Majú rovnaké aj telesové výšky. Ako vieme, telesová výška ihlana je vzdialenosť jeho hlavného vrcholu od roviny podstavy. V ihlane ABCDF je telesovou výškou hrana BF, lebo je kolmá na podstavu ABCD. Hrana EF je kolmá na ľavú bočnú stenu kocky, preto bude výškou v ihlane ADHEF. V poslednom ihlane CDHGF je telesovou výškou hrana FG. To preto, lebo táto hrana je kolmá na zadnú stenu kocky. Každá z týchto telesových uhlopriečok má dĺžku, ktorá je rovnaká ako dĺžka hrany kocky. Uvažované tri štvorboké ihlany majú teda zhodné podstavy a telesové výšky. Sú zhodné. Zhodné telesá majú rovnaký objem, preto je objem jedného z ihlanov tretinou objemu kocky. Potom sa dá táto finta využiť aj pre iné hranoly ako kocka, ale nemusí to byť také jednoduché. Pre predstavu to ale stačí.
Vzorec pre objem hranola je V = Sp.v. Žiaci si teda budú pamätať, že do hranola sa zmestia tri ihlany s rovnakým objemom. Preto sa objem ihlana s rovnakou podstavou ako je podstava hranola a s rovnakou telesovou výškou vypočíta podľa vzorca: